Laplace Transform is necessary in the control world.
It is necessary to solve linear ODE, linear ODE system including initial value problem.
How to solve?
1. 주어진 ODE를 보조방정식(subsidiary equation)으로 변환한다.
2. 보조방정식을 대수적으로 풀어 해를 얻는다.
3. 위의 해를 역변환한다.
Definition
$$F(s)=\mathcal{L}(f)=\int_{0}^{\infty}{e^{-st}f(t)dt}$$
Examples
| $$f(t)$$ | $$\mathcal{L}(f)$$ | $$f(t)$$ | $$\mathcal{L}(f)$$ |
| $$1$$ | $$ \frac{1}{s} $$ | $$\cos wt$$ | $$\frac{s}{s^2+w^2}$$ |
| $$t$$ | $$\frac{1}{s^2}$$ | $$\sin wt$$ | $$\frac{w}{s^2+w^2}$$ |
| $$t^n$$ | $$\frac{n!}{s^{n+1}}$$ | $$\cosh at$$ | $$\frac{s}{s^2-a^2}$$ |
| $$t^a (a>0)$$ | $$\frac{\Gamma(a+1)}{s^{a+1}}$$ | $$\sinh at$$ | $$\frac{a}{s^2-a^2}$$ |
| $$e^{at}$$ | $$\frac{1}{s-a}$$ | $$e^{at}\cos wt$$ | $$\frac{s-a}{(s-a)^2+w^2}$$ |
| $$e^{at}\sin wt$$ | $$\frac{w}{(s-a)^2+w^2}$$ |
Properties
1. Superposition
$$\mathcal{L}\left\{ \alpha f_1(t)+\beta f_2(t)\right\}=\alpha F_1(s)+\beta F_2(s)$$
2. Time Delay
$$F_1(s)=\int_{0}^{\infty}f(t-\lambda)e^{-st}dt=e^{-s\lambda}F(s)$$
$$\mathcal{L} \left\{ f(t-a)u(t-a) \right\}=e^{-as}F(s)$$
$$or\quad \mathcal{L} \left\{ f(t)u(t-a) \right\}=e^{-as}\mathcal{L}\left\{ f(t+a) \right\}$$
3. Time Scaling
$$F_1(s)=\int_{0}^{\infty}f(at)e^{-st}dt=\frac{F(\frac{s}{a})}{\left|a \right|}$$
4. Shift in Frequency
$$F_1(s)=\int_{0}^{\infty}e^{-at}f(t)e^{-st}dt=F(s+a)$$
5. Differentiation
$$\mathcal{L}\left\{ \dot{f} \right\}=sF(s)-f(0^-)$$
$$ \mathcal{L}\left\{ \ddot{f} \right\}=s^2F(s)-sf(0^-)-\dot{f}(0^-)$$
$$\mathcal{L}\left\{ f^{(m)} \right\}=s^mF(s)-s^{m-1}f(0^-)-s^{m-2}\dot{f}(0^-)-\cdots -f^{(m-1)}(0^-)$$
6. Integration
$$ \mathcal{L}\left\{ \int_{0}^{t} f(\xi)d\xi \right\}=\frac{F(s)}{s}$$
7. Convolution
$$(f*g)(t)=\int_{0}^{t}f(\tau)g(t-\tau)d\tau$$
$$ \mathcal{L}\left\{ f_1(t)*f_2(t) \right\}=F_1(s)F_2(s)$$
8. Time Product
$$ \mathcal{L}\left\{ f_1(t)f_2(t) \right\}=\frac{F_1(s)*F_2(s)}{2\pi j}$$
9. Multiplication by Time
$$\mathcal{L}\left\{ tf(t) \right\}=-\frac{\mathrm{d} }{\mathrm{d} s}F(s)$$
10. Divisiton by Time
$$ \mathcal{L}\left\{ \frac{f(t)}{t} \right\}=\int_{s}^{\infty}F(\tilde{s})d\tilde{s}$$
Unit Step function (Heaviside function)
$$u(t-a)=\left\{\begin{matrix}
0,\quad t<a \\ 1,\quad t>a
\end{matrix}\right.$$
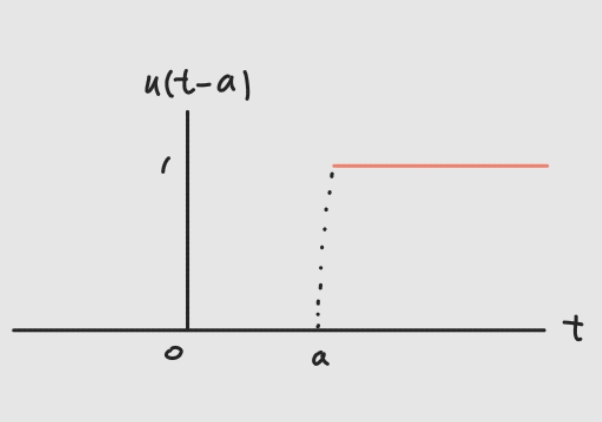
$$\mathcal{L} \left\{ u(t-a) \right\}=\frac{e^{-as}}{s}$$
Unit Impulse function (Dirac Delta function)
$$\delta (t-a)=\left\{\begin{matrix}
\infty, \quad t=a \\ 0, \quad else
\end{matrix}\right.
\quad and \quad \int_{0}^{\infty}\delta (t-a)dt=1$$
$$\mathcal{L}\left\{ \delta(t-a) \right\}=e^{-as}$$
Transfer Function
Transfer Gain from $U(s)$ to $Y(s)$ - input to output.
Ratio of the Laplace Transform
$$H(s)=\frac{Y(s)}{U(s)}$$
ex 3.4)
find the output $y$ for the input $u=e^{st}$
system eqn: $\dot{y}(t)+ky(t)=u(t)=e^{st}$
assume that $y(t)=H(s)e^{st}$
$sH(s)e^{st}+kH(s)e^{st}=e^{st}\to H(s)=\frac{1}{s+k}\to y=\frac{e^{st}}{s+k}$
ex 3.6)
step & ramp transforms
step of size $a$: $F(s)=\int_{0}^{\infty}ae^{-st}dt=\frac{a}{s}$
ramp $bt$: $F(s)=\int_{0}^{\infty}bte^{-st}dt=\frac{b}{s^2}$
'Study > Control' 카테고리의 다른 글
| State-Space Design (0) | 2025.01.30 |
|---|---|
| Frequency-Response Design (0) | 2025.01.15 |
| Root Locus, Compensation (0) | 2025.01.13 |
| PID Control (1) | 2025.01.04 |
| Introduction: the Fundamentals of Control Theory (0) | 2024.12.28 |